Stochastic Gradient Descent & Hill Climbing

Starting with random walk, we came up with another pair of local search algorithms that are significantly more efficient: gradient descent and hill climbing. But they aren't perfect. Although they terminate much faster, they can get stuck in local minima or maxima, failing to return a global minima or maxima. So how can we fix this? There are different variations on the basic gradient descent and hill climbing algorithms that can help an agent avoid getting trapped in local minima or maxima, depending on the context.

To simplify the discussion, we'll explain these varieties by building off of gradient descent, but the same ideas apply to hill climbing as well.

Steepest-Descent

The basic version of gradient descent we've looked at so far is called steepest-descent. Recall, the core idea behind steepest-descent is to choose the lowest-valued neighbor from each state during the search. Intuitively, this makes sense. If an agent is in a state surrounded by $n$ neighbors, the one with the lowest cost likely offers the "steepest" (or "fastest") path to the global minimum. It's a greedy approach that can work pretty well, but as we discovered in an earlier post, it might lead to a suboptimal solution.

Stochastic Gradient Descent

The reason that the steepest-descent version of gradient descent has a propensity to converge to a local minimum is because greedily transitioning to the lowest-valued neighbor can be helpful in the short-term, but prevents the agent from exploring other parts of the state space that might have a better chance of leading to a global minimum. Consider the following state in the fire station location problem:

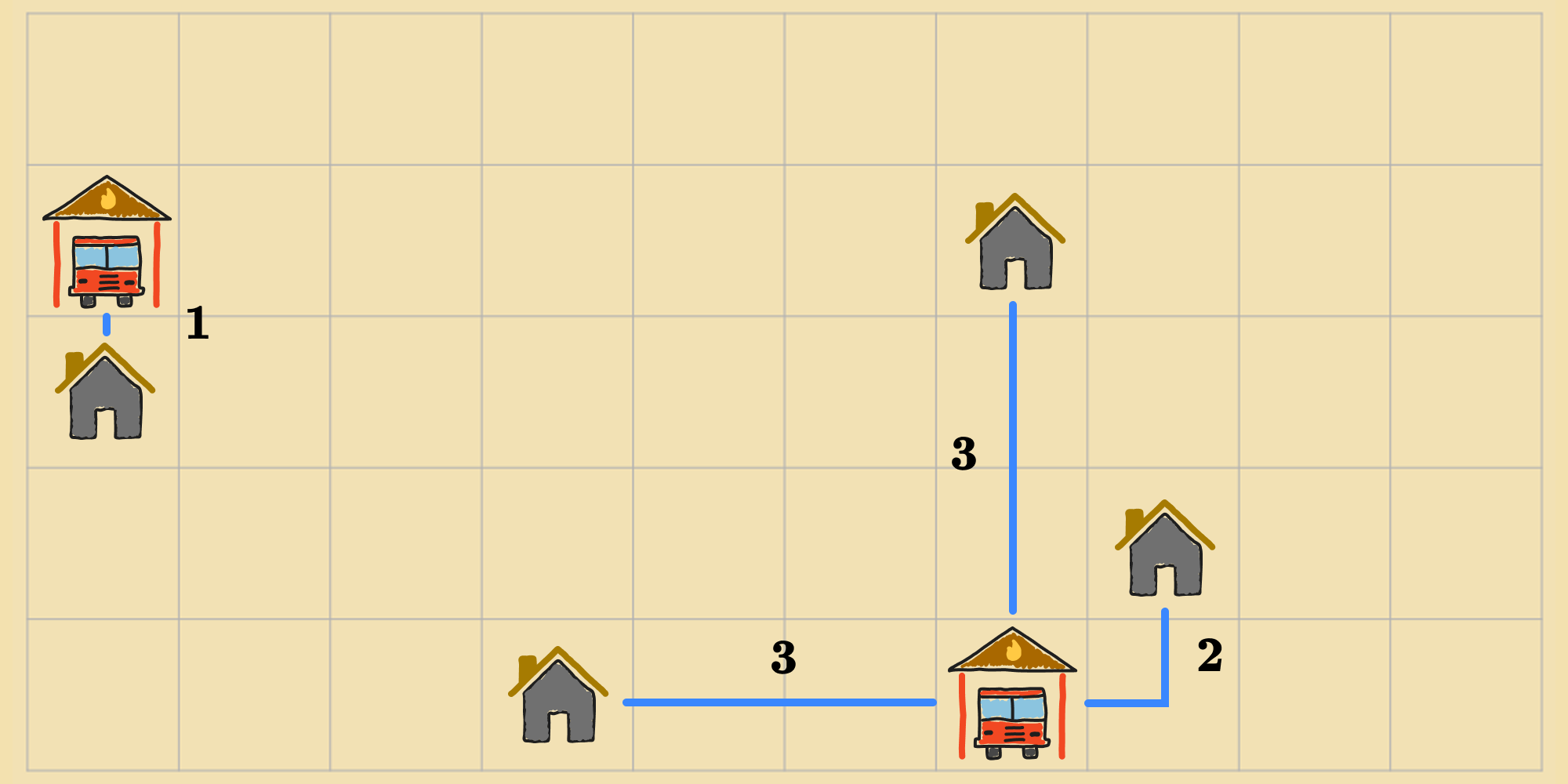
If the agent is following a steepest-descent approach, it will terminate immediately and return this current state, because it's surrounded by neighbors that are either equal or worse.

But, there are other states that are more optimal, e.g.:

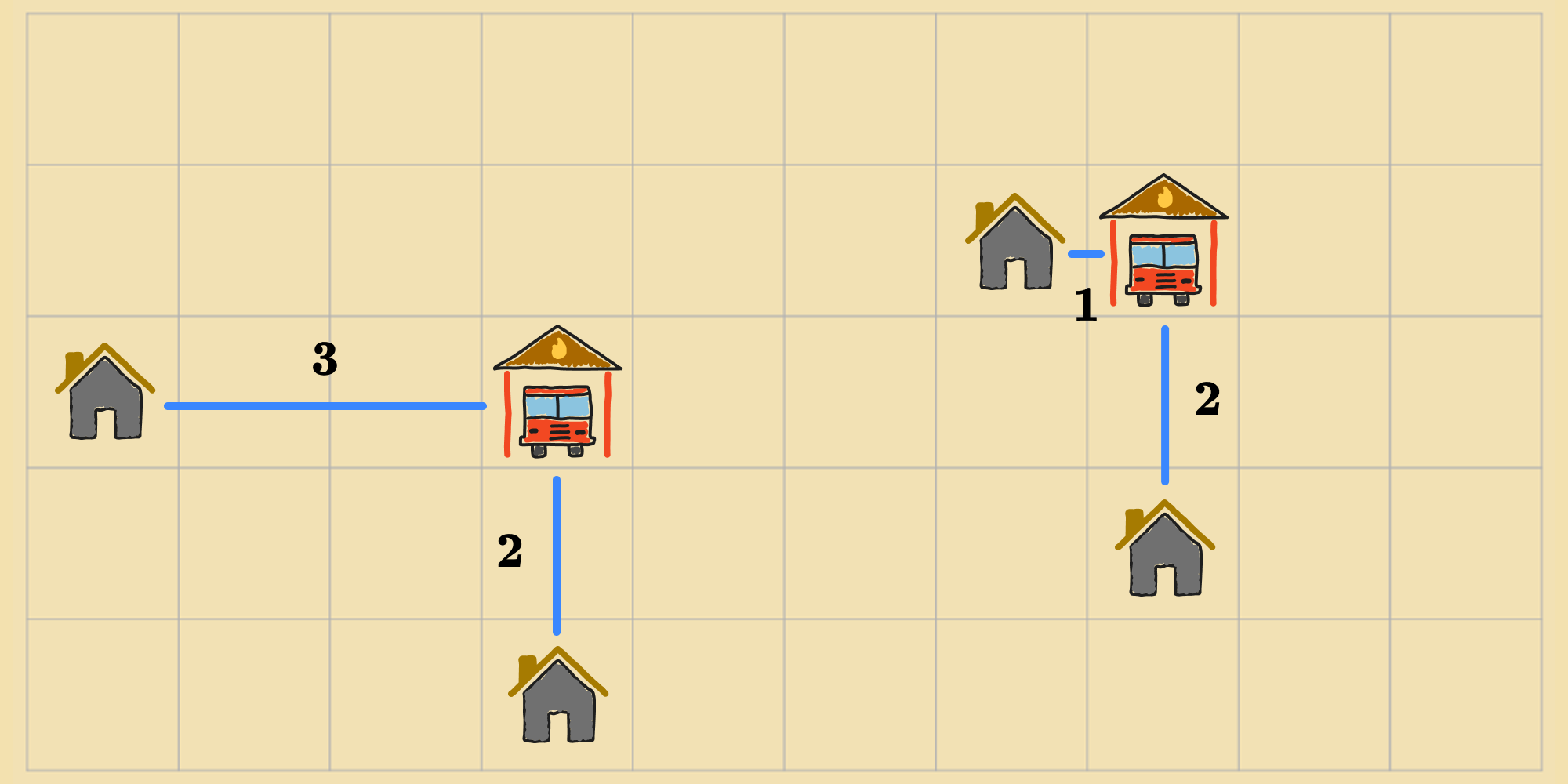
To address this limitation, we can give the agent more latitude in action selection so that it can explore regions of the state space with opportunities to bypass local minima.

Just like we improved random walk by maintaining the same search loop, but enhancing how the agent chooses actions, we can improve steepest-descent by maintaining the structure, but updating how the agent selects from its neighbors. Instead of always moving to the "best" neighbor, the agent can randomly pick from any neighbor with lower cost, not just the lowest cost one. The probability of choosing a particular neighbor can be proportional to the steepness of the downhill move. This flavor is known as stochastic gradient descent (SGD).

$$\begin{aligned} &\textbf{function}\ \text{STOCHASTIC-GRADIENT-DESCENT}(s_0, f, \text{ACTIONS}, \text{RESULT}, \\ &\quad \text{MAX-SIDEWAYS}): \\ &\quad s \gets s_0 \\ &\quad count_{sideways} \gets 0 \\ &\quad \textbf{while}\ \text{true}\ \textbf{do} \\ &\quad\quad a^* \gets \text{SAMPLE}(a \in \text{ACTIONS}(s) | f(\text{RESULT}(s, a)) \le f(s)) \\ &\quad\quad s^* \gets \text{RESULT}(s, a^*) \\ &\quad\quad \textbf{if}\ f(s^*) < f(s)\ \textbf{then} \\ &\quad\quad\quad \textbf{return}\ s \\ &\quad\quad \textbf{else if}\ f(s^*) = f(s)\ \textbf{then} \\ &\quad\quad\quad count_{sideways} \gets count_{sideways} + 1 \\ &\quad\quad\quad \textbf{if}\ count_{sideways} > \text{MAX-SIDEWAYS}\ \textbf{then} \\ &\quad\quad\quad\quad \textbf{return}\ s \\ &\quad\quad\quad \textbf{end if} \\ &\quad\quad \textbf{end if} \\ &\quad\quad s \gets s^* \\ &\quad \textbf{end while} \\ \end{aligned}$$

The parameter $\text{MAX-SIDEWAYS}$ is necessary to prevent the agent from looping indefinitely. Without it, the agent could find itself moving between neighboring states that are global minima.

By operating probabilistically, SGD lives somewhere between steepest-descent and random walk. It's more lax than steepest-descent, choosing amongst any neighbor that improves the objective function—the premise being that any neighbor that makes forward progress could lead to a global minimum, even though it's not locally the best—but not as random as random walk, which indiscriminately chooses neighbors, regardless of their cost. SGD usually converges more slowly than steepest-descent, but in some state-space landscapes, it can find a better solution.

First-Choice Gradient Descent

First-choice gradient descent behaves in a similar way. It samples from the neighbors of the current state with equal probability, until it finds a candidate successor that has a lower cost. This is more practical when the number of successor states for each state is large (e.g. tens of thousands of neighbors). Rather than consider all of the neighbors, as soon as the agent finds a neighbor that is better than its current state, it will move to that neighbor. This can be more efficient than SGD, as it doesn't need to consider all neighbors before making a decision.

Random-Restart

"If at first you don't succeed, try, try again."

Although it helps, SGD doesn't eliminate the risk that the agent might end up at a local minimum. We can further reduce this risk by simply repeating the search multiple times. Random-restart gradient descent simply runs SGD multiple times, each time starting from a different random state. The agent tracks the best state it has found so far from each run, and if the next run returns a better state, it will replace the current best state. After all runs have completed, the agent returns the best state it has found.

$$\begin{aligned} &\textbf{function}\ \text{RANDOM-RESTART}(f, \text{ACTIONS}, \text{RESULT}, \\ &\quad \text{MAX-SIDEWAYS}, \text{NUM-ITERATIONS}): \\ &\quad s_{best} \gets \text{null} \\ &\quad \textbf{for}\ i \gets 1 \text{ to } \text{NUM-ITERATIONS} \textbf{ do} \\ &\quad\quad s_0 \gets \text{SAMPLE}(\text{STATES}) \\ &\quad\quad s \gets \text{STOCHASTIC-GRADIENT-DESCENT}(s_0, f, ...) \\ &\quad\quad \textbf{if}\ f(s) < f(s_{best})\ \textbf{then} \\ &\quad\quad\quad s_{best} \gets s \\ &\quad\quad \textbf{end if} \\ &\quad \textbf{end for} \\ &\quad \textbf{return}\ s_{best} \\ \end{aligned}$$

Random-restart will converge to a global minimum with probability $1$ over infinite runs, because it will eventually generate an optimal state as the initial state. But that's not practical. If each search has a probability $p$ of success, then the expected number of restarts required is $1/p$. So it's not a panacea, but it can dramatically improve the chances of finding a global minimum.

Summary

The shape of the state-space landscape is a key determinant to the success of gradient descent (and hill climbing)—and the variants we've covered. And depending on the nature of the landscape, some of these variants might be more successful than others. For example, if there are a lot of local maxima, random-restart gradient descent might not find an optimal solution, or it might take a long time. Despite this, a reasonably good local minimum (or maximum) can often be found by combining SGD with random restarts in many cases.