Global vs Local Optimums

Weaknesses of Gradient Descent & Hill Climbing

Now that we're armed with gradient descent (and its complement, hill climbing), we have a good tool for solving optimization problems. It's a big improvement over random walk in terms of how efficiently it allows the agent to explore the state space. But, do gradient descent and hill climbing always find the best possible solution? Do they guarantee that we'll find the optimal state that achieves the minimum or maximum of the objective function? Let's investigate by revisiting the fire station location problem (introduced in this post). Suppose this is the initial state $s₀$ of our agent, with a cost of $17$:

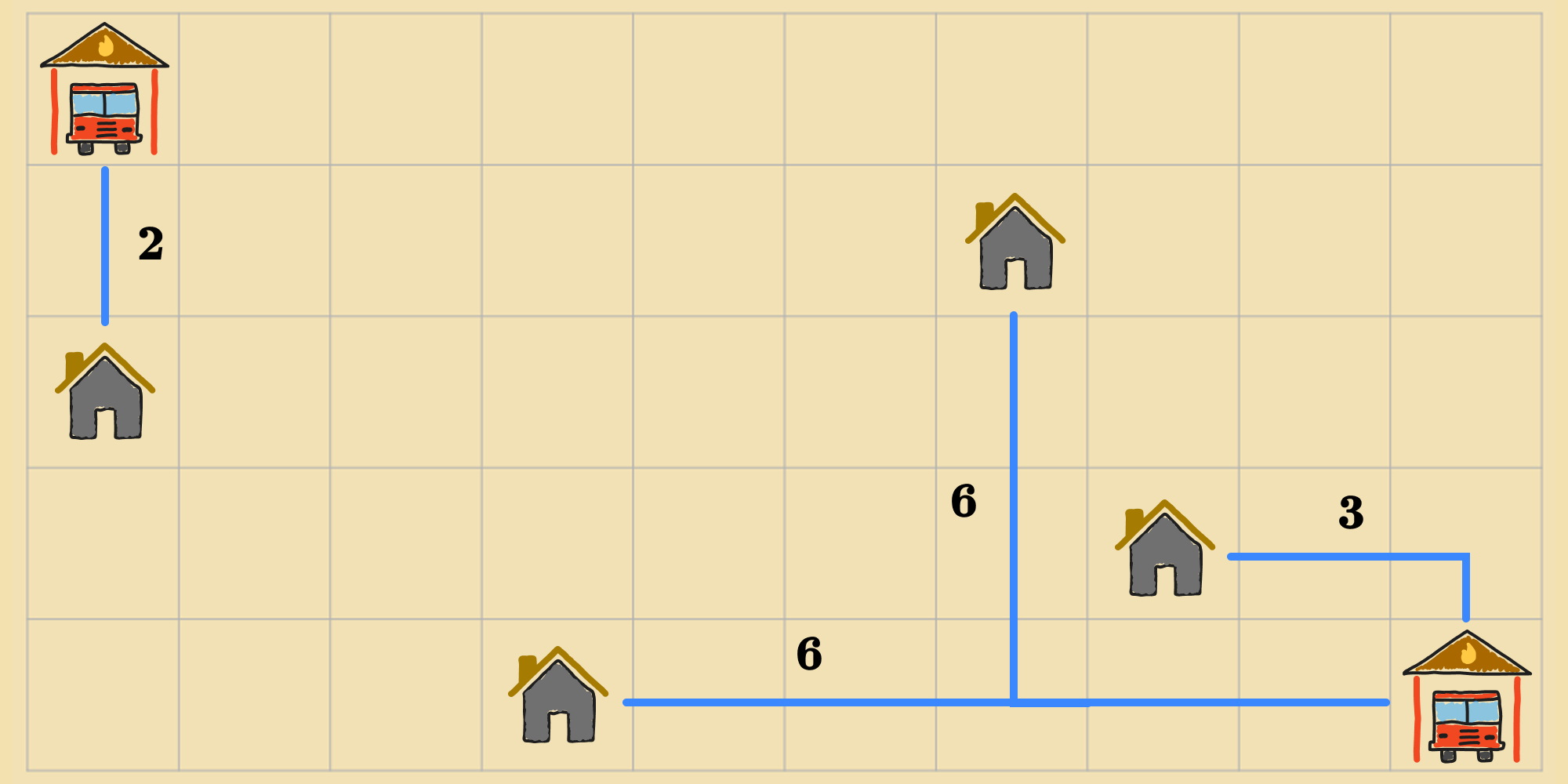
If our agent is running gradient descent, it will transition to the following state, which has the lowest value according to the objective function ($14$), relative to the neighbors.

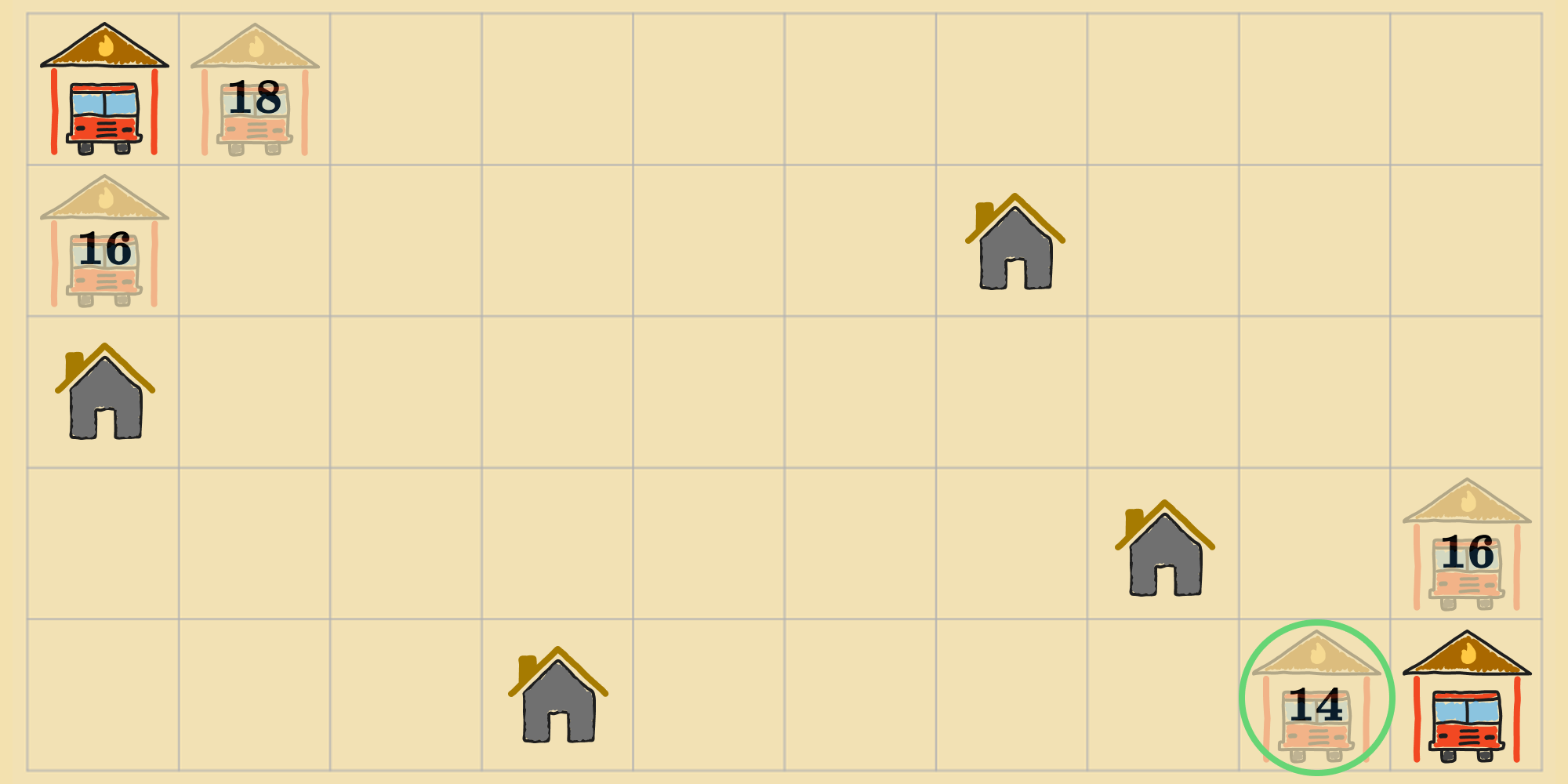
If the agent continues to run gradient descent from this new state, it will eventually settle into the following state, which has a cost of $9$.

At this point, the process terminates, and this state—let's call it $s'$—is returned as the solution because none of its neighbors improve the objective function. But, is this the best placement of fire stations? Think about it for a moment...

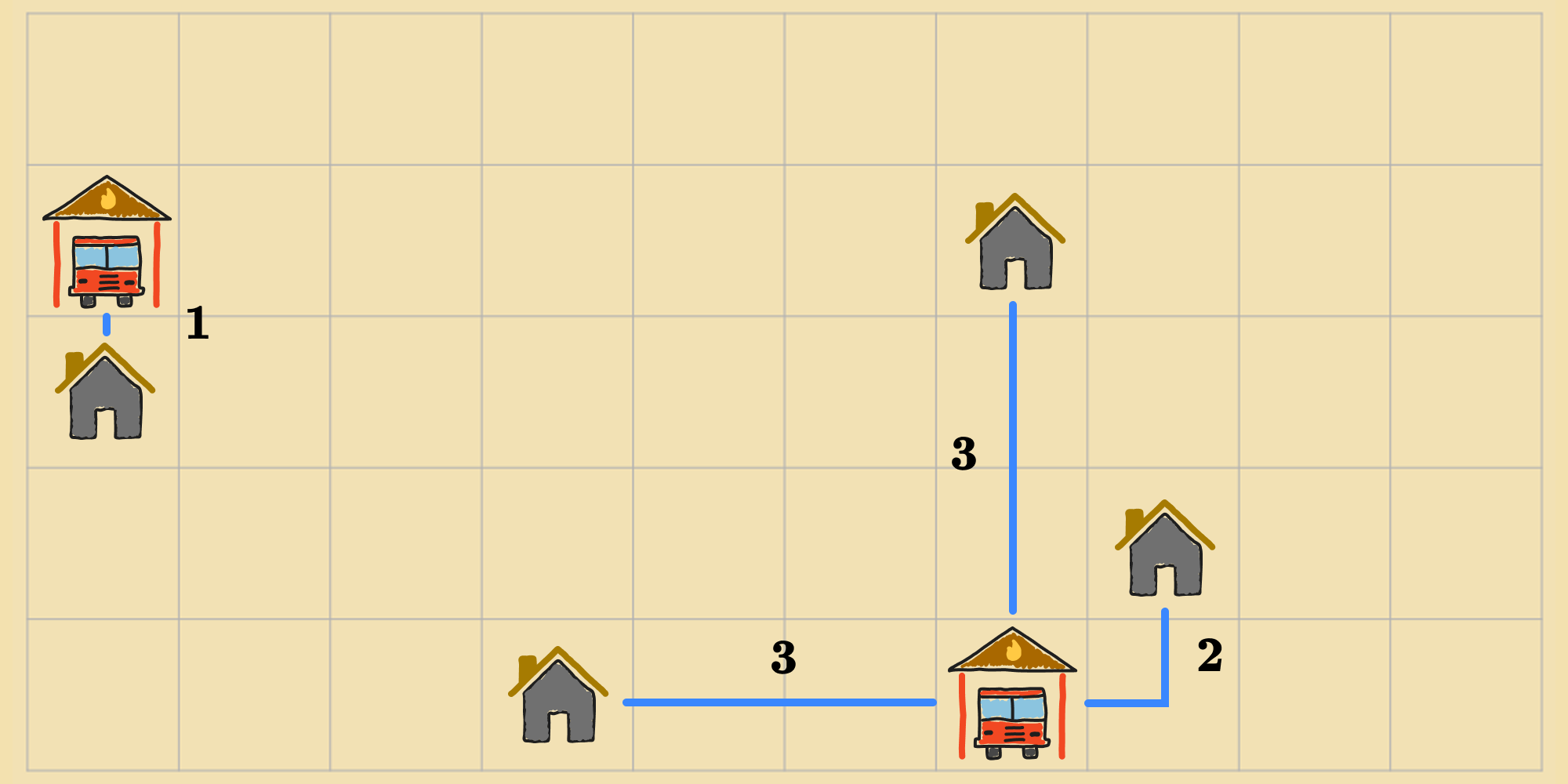
The answer is no. Consider this alternative positioning.

The cost of this state—$s^*$—is $8$, which is better than $f(s')$. So why did gradient descent stop before exploring this state? It's because $s^*$ is on the other side of the "wall" of neighbors surrounding $s'$, which each have an equal or higher cost.

This is a limitation of gradient descent and hill climbing, arising from the fact that they are local search algorithms that don't look beyond the immediate neighbors of a state when making decisions. Any state like $s'$ is called a local minimum, where all of the neighboring states have equal or higher cost, but it's not the best state. The best state, $s^*$, is called a global minimum, where all other states in the state space have equal or higher cost, not just the neighbors. Our agent is looking for the global minimum, but can get stuck in a local minimum if it's using gradient descent naively, starting from a bad initial state.

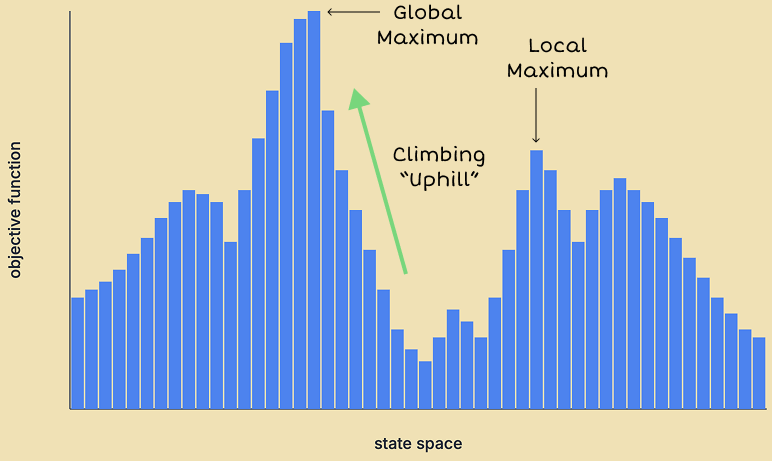
For problems looking to find the state corresponding to the maximum value of some objective function—i.e. where we'd apply hill climbing—we have the reverse concepts of local maximum and global maximum. A state is a local maximum when all of its neighboring states have equal or lower value, but the state is not the highest-value state. A state is a global maximum when all other states in the state space have equal or lower value.

State-Space Landscape

We can visualize optimization problems as a state-space landscape, and to introduce the concept, lets consider a simplified version of the fire station problem, where we only have one fire station and the houses are situated on a 1D line instead of a 2D grid.

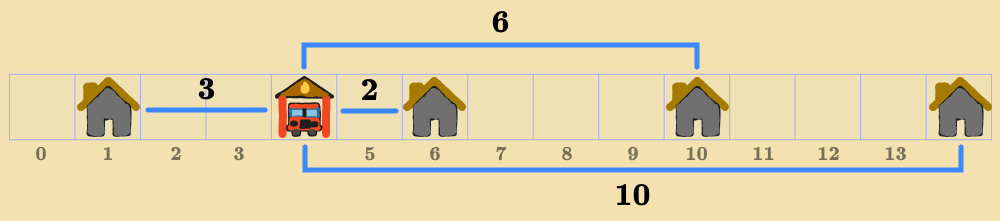
Here's the formal description of the problem:

• States ($S$): The set of all possible points along the line that are empty (i.e. not occupied by a house).
• Initial State ($s₀$): The starting location of the fire station.
• Objective Function ($f$): The sum of the Manhattan distances from each house to the fire station.
• Actions ($\text{ACTIONS}(s)$): Move the fire station one square, left or right, as long it's not at the end of the 1D town. If there's a house on either side of the fire station, then an action simply moves it to the other side of the house, as long as the square is free.
• Transition Model ($\text{RESULT}(s, a) → s'$): New state resulting from shifting the fire station by one unit.

Now we can represent the state-space as a plot, where each point on the x-axis represents a possible location for the fire station, with a vertical bar whose height is the value of the objective function.

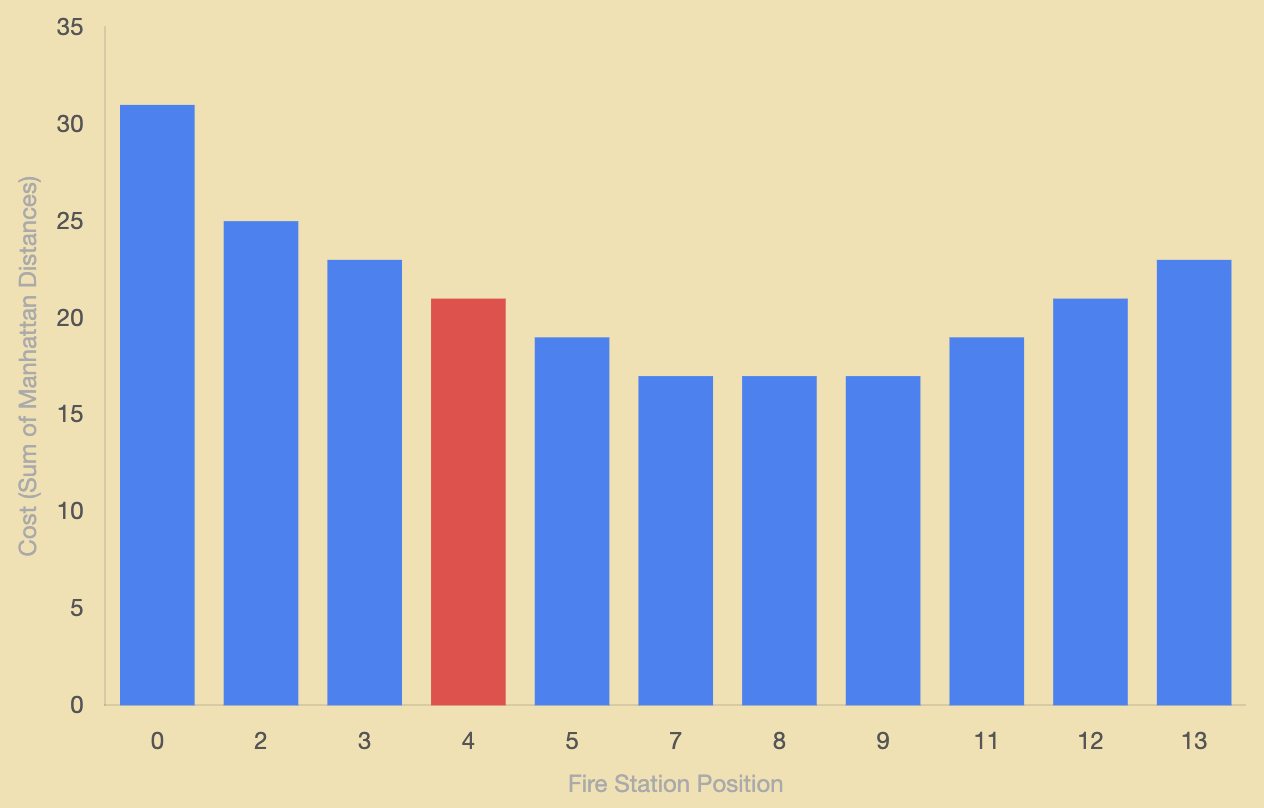
We arrange the states along the axis so that the points to the left and right of a state are its neighbors in the state-space. The resulting graphical representation is a state-space landscape. More abstractly, the state-space landscape is a plot of the objective function over the state-space, where states are arranged so that neighbors are adjacent to each other. We can imagine more complex landscapes for other problems, with different states, actions, objective functions, and transition models—and therefore, different notions of neighbors.

Referring back to gradient descent, we can view it as the agent "descending" down the landscape, until it reaches the "bottom of a valley". At any point corresponding to the agent's state, it considers the local landscape formed by its neighbors, and moves "downhill" to the neighbor at the bottom of the steepest slope. It keeps moving downhill until there's no longer any downward slope to take it further, i.e. each of its neighbors are no better than the current state. If the bottom belongs to the deepest valley, then the agent has found a global minimum. Otherwise, it's stuck in a local minimum.

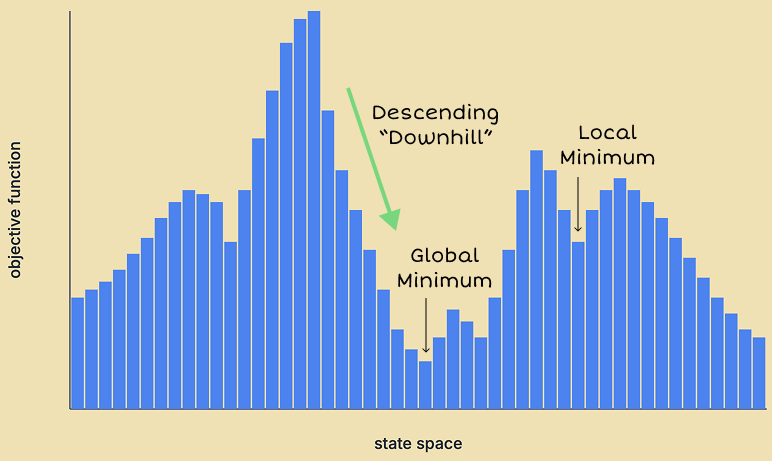
Similarly, hill climbing can be interpreted as the agent "climbing up a hill" in the landscape until it reaches a "peak". If the peak belongs to the tallest hill, then the agent has found a global maximum, but otherwise, it's a local maximum.

Final Thoughts

So the takeaway is when we run a naive gradient descent or hill climbing algorithm, we're not always going to find the optimal solution. Whether the agent finds the global minimum or maximum is sensitive to the initial state. From a poor starting state, the momentum of gradient descent or hill climbing can carry the agent to a local minimum or maximum, where it will get stuck.