Intro to Optimization

When Goals are Hard to Define

The objective of search is to find a path of actions and states that takes an agent from an initial state to a goal state. This assumes we can specify all the goal states $G$ so that when the agent is in the search process, we can easily check if a state it's occupying corresponds to a goal. For example, in maze navigation, the goal state is exiting the maze.

With 8-puzzle, the goal state is a configuration of tiles that are ordered numerically.

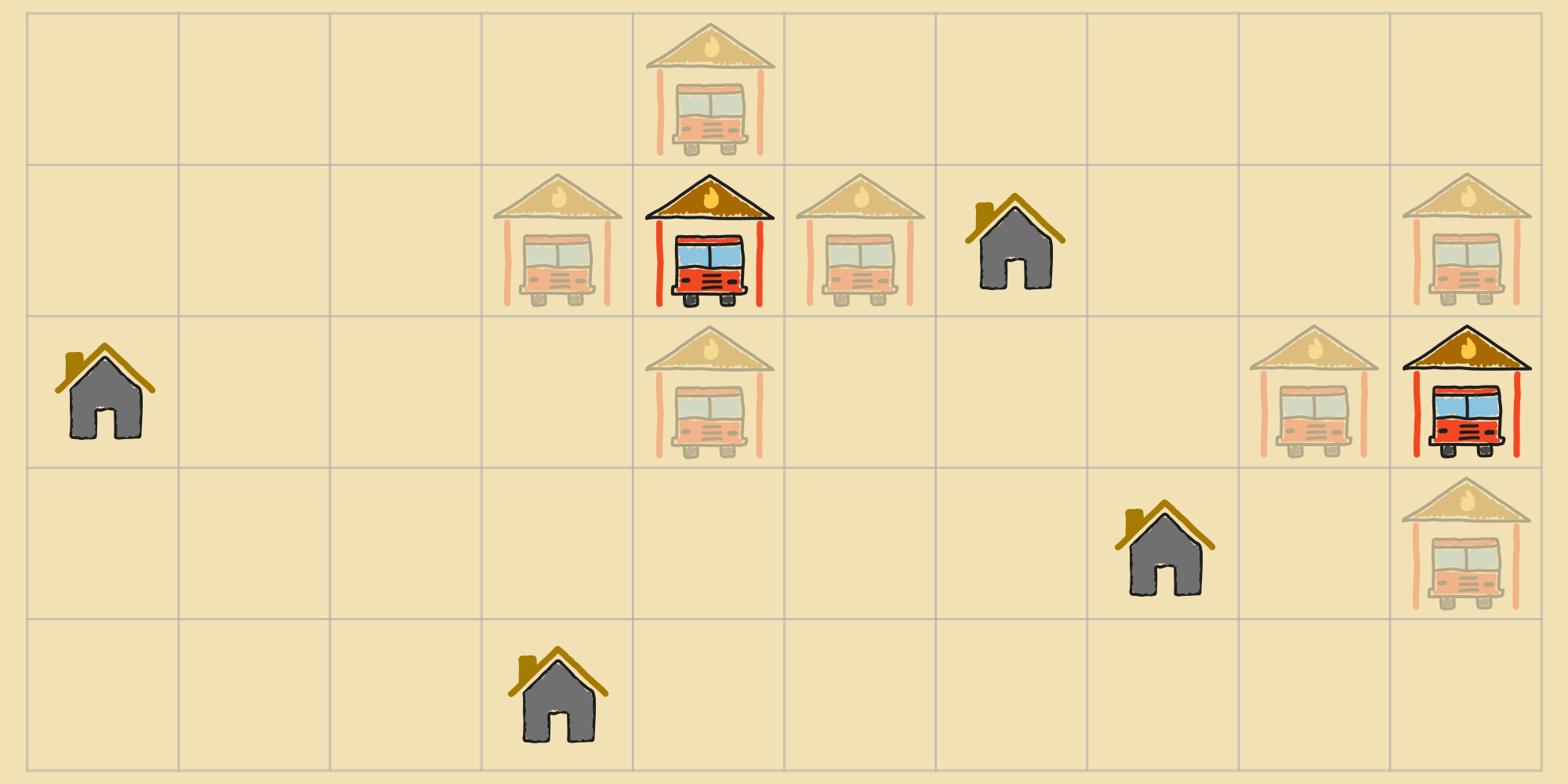
In both cases, it's obvious whether or not the agent has achieved the goal. But what if the goal state can't be specified in an explicit way? Consider the following problem: A new town, organized as a 2D grid with a bunch of houses, is planning to build two fire stations to serve the residents of the town. But they don't want to build the stations at arbitrary locations. Instead, they want to place the stations at locations that minimize how far the fire trucks have to travel to reach each house. The distance in this grid town is measured using Manhattan distance.

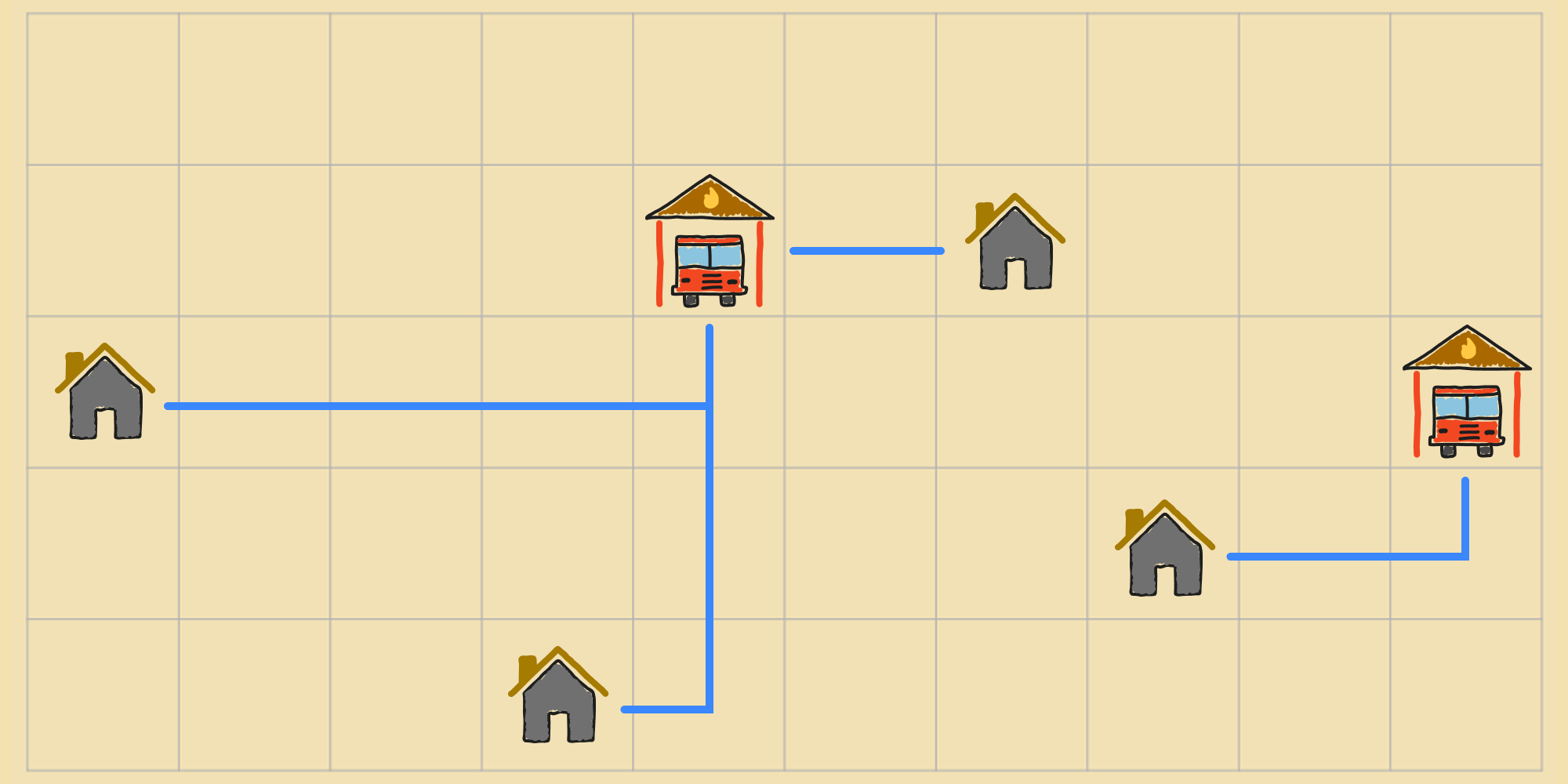
Now until we find an ideal placement for the fire stations, we can't readily point to any state, i.e. configuration of fire stations on the grid, as the goal. If we could, then the problem would be trivial. But instead of identifying the goal states a priori, we can try to measure how close a state is to the goal.

Lets say we use the sum of the Manhattan distances from each house to the nearest fire station as our measure—or lets call it—objective function. The value of the objective function for this state is $14$ ($= 5 + 4 + 2 + 3$).

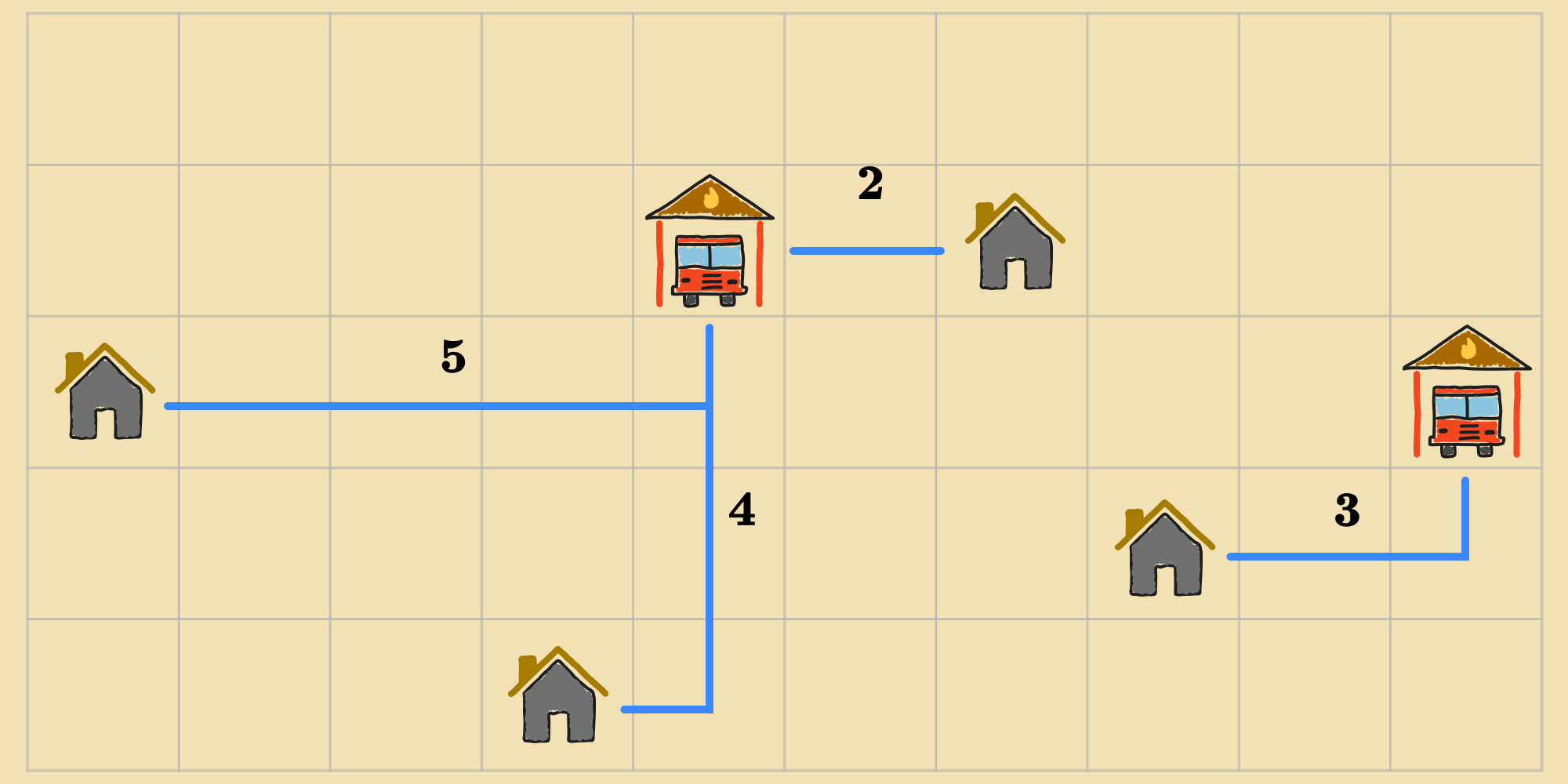
For this other state, the value—or cost—is $14$ ($= 3 + 4 + 4 + 3$).

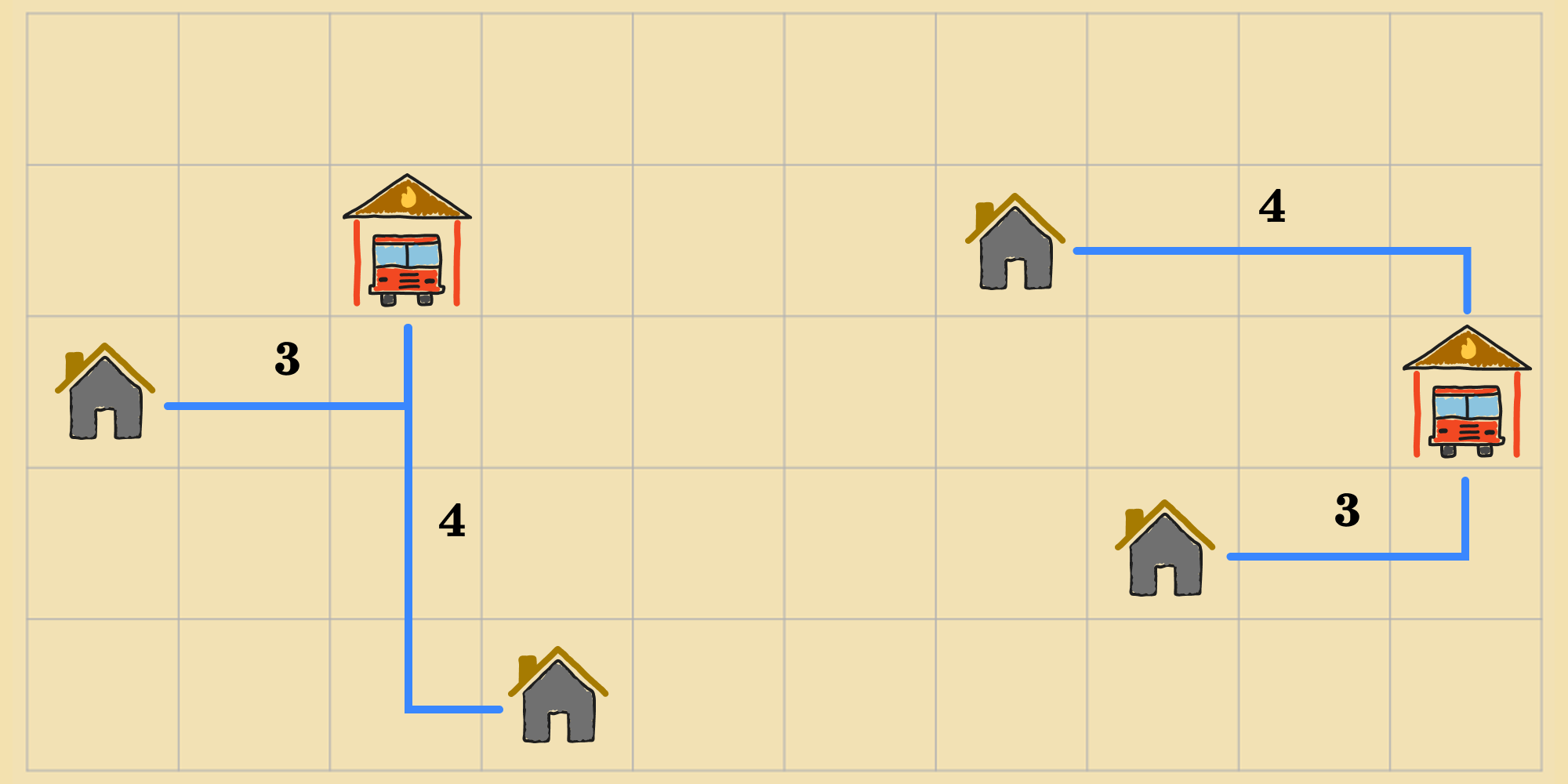
The lower the value of a state, the better it is because it means its closer to an optimal state, i.e. a state where the distance between each residence and the closest fire station is minimized. Now, the objective function doesn't only give us a way to calculate the "quality" of a state, but we also have a way to express the goal states: Any state the achieves a minimum value according to the objective function is a goal state. We can modify approaches to search by traversing the state space and calculating the cost of each state as we go, until we find a state with the lowest cost as defined by the objective function.

Optimization

This fire station problem is an example of an optimization problem. Optimization is about finding the best option from a set of possible options that balances a set of trade-offs. In other words, it's about finding the best state in a state space, one that optimizes (minimizes or maximizes) an objective function which captures the trade-offs. For planning where to build fire stations, we're optimizing for total distance from each house to its nearest station, where shifting a fire station closer to one home may shift it further away from another home.

Problem Formulation

We can use the same formal structure as a search problem, except that we replace the goal states $G$ with an objective function $f$, which measures the distance or closeness of a state with respect to the minimum or maximum value of $f$, which corresponding to our goal states.

• States ($S$): The state space consisting of all possible states of the environment.
• Initial State ($s₀$): The starting point.
• NEW → Objective Function ($f$): A function that maps a state $s$ to a real number, representing how far or close $s$ is to the the optimal state. A well-crafted objective function captures the trade-offs of the problem in a way where solving for the minimum (or maximum) leads the agent to a goal state.
• Actions ($\text{ACTIONS}(s)$): For each state $s$, the set of actions that can be executed when the agent is in $s$.
• Transition Model ($\text{RESULT}(s, a) → s'$): A function that describes what each action does by mapping a state $s$ and an action $a$, to the resulting state $s'$.

So we can formally describe the fire station location problem:

• States ($S$): The set $(x_1, y_1), (x_2, y_2)$ of all possible pairs of locations for the fire stations on the map.
• Initial State ($s₀$): The starting locations of each fire station.
• Objective Function ($f$): Represents the total Manhattan distance from each house to the nearest fire station.
• Actions ($\text{ACTIONS}(s)$): Move one of the fire stations one unit in any permitted direction.

• Transition Model ($\text{RESULT}(s, a) → s'$): New state resulting from shifting one of the fire stations by one unit.

In classic search problems, we're interesting in finding a path to an objective state, but in optimization settings, we're less interested in the path. Rather, the challenge is to find out which state satisfies our objective:

$$G = \arg\min_{s \in S} f(s) \quad \text{ or } \quad G = \arg\max_{s \in S} f(s)$$