Local Beam Search

The great thing about the local search algorithms we've covered so far—from random walk, to gradient descent and hill climbing, and their variants—is that their memory footprint is small. They only need to store the current state and the best state they've found so far, so the memory usage is $O(1)$ . But the more memory we give an agent, the more it can explore, and the more likely it is to find a global minimum or maximum. Local beam search is a generalization of gradient descent and hill climbing that keeps track of $k$ states simultaneously, rather than just one.

Local Beam Search

Lets return to our running example of optimizing the locations of fire stations in a city. We'll use local beam search to place the fire stations such that the total distance of each home to its nearest fire station is minimized.

Local beam search works by randomly picking $k$ initial states. Lets say $k = 2$ for our example.

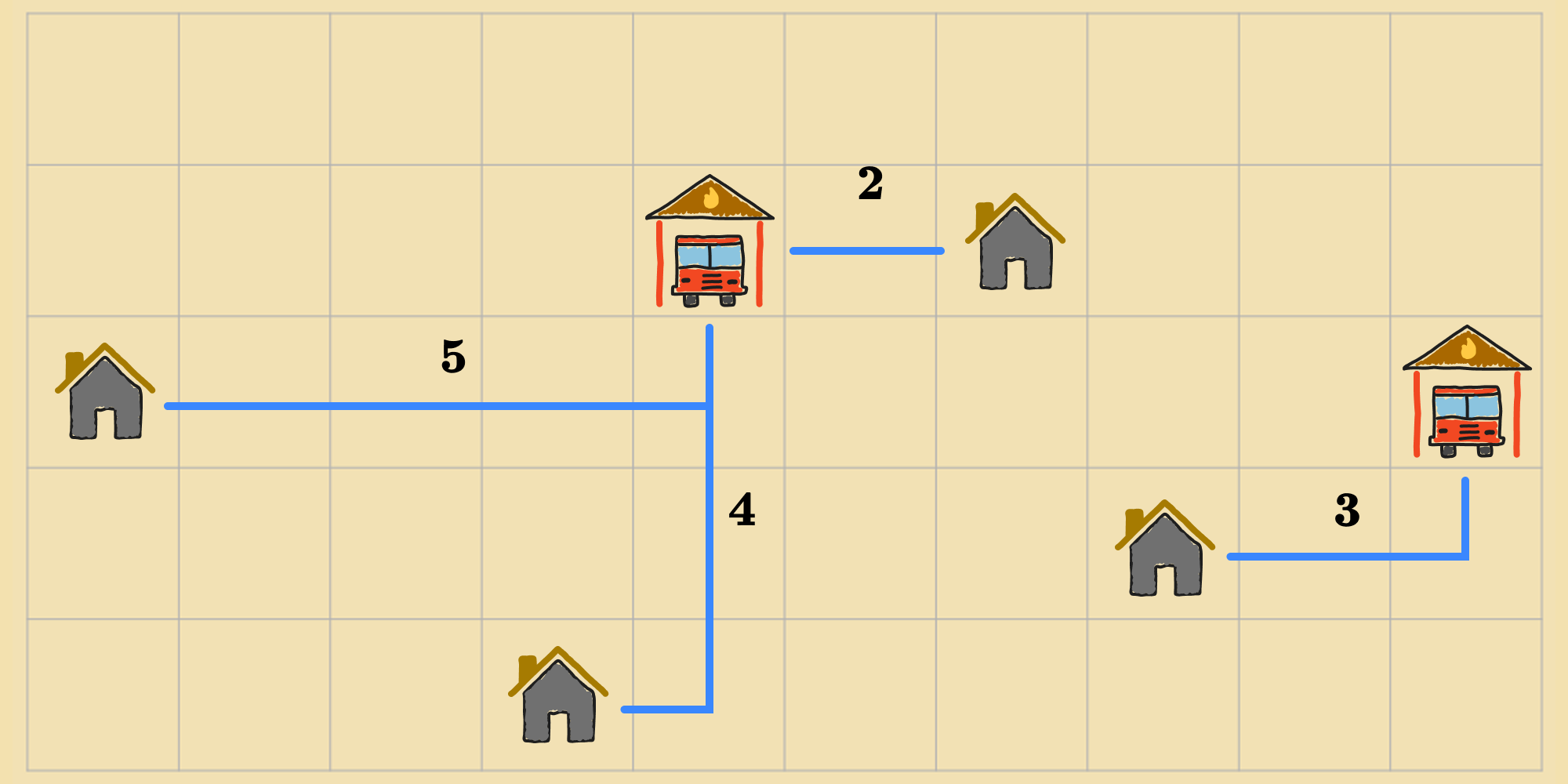
First initial state

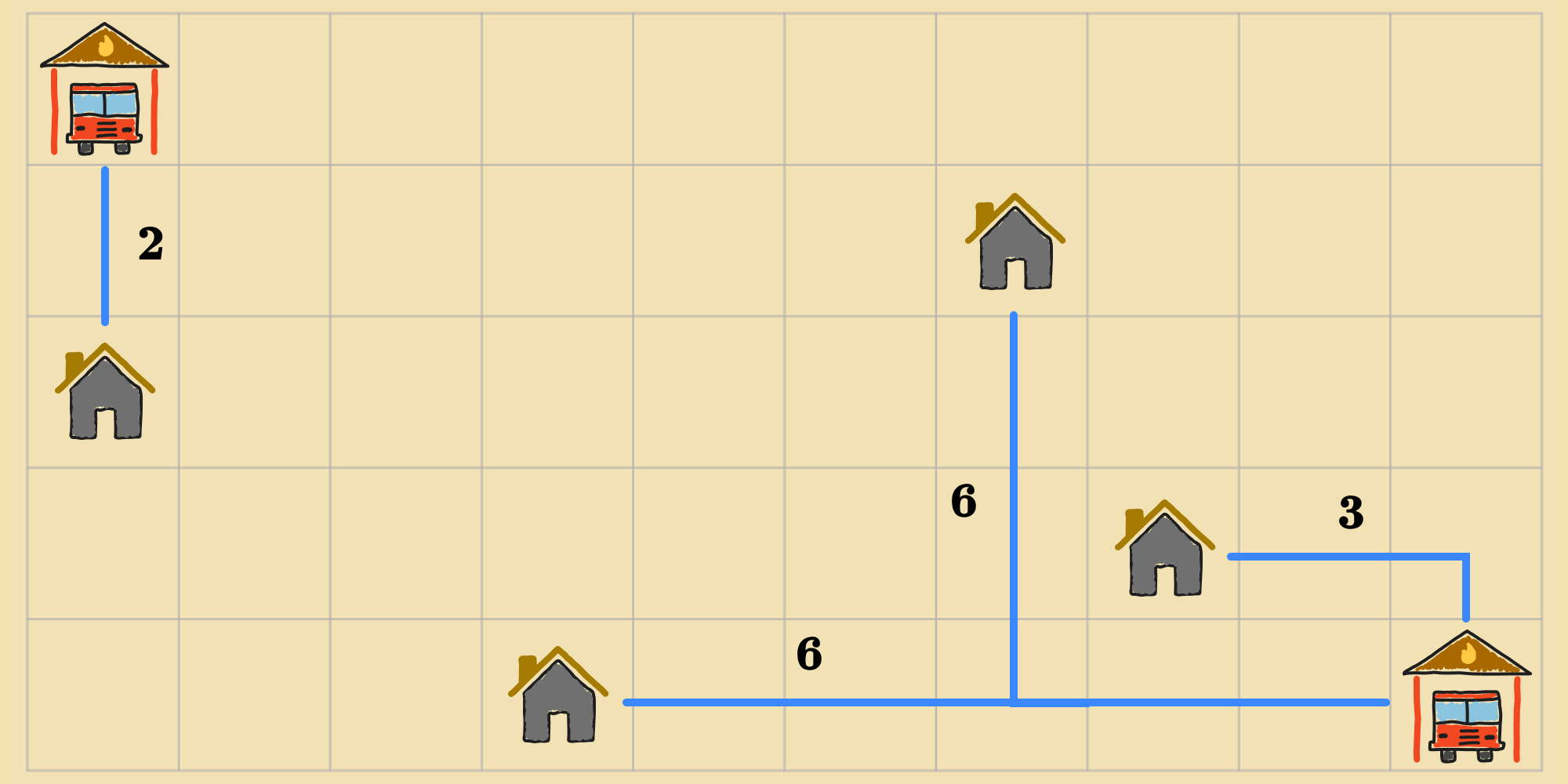
Second initial state

At each step, all the successors of all $k$ states are generated. This is just like how previous algorithms would find the successors of the agent's current state during each iteration. From this set of successors, the agent selects the $k$ best states, according to the objective function (if there's a tie amongst more than $k$ states, the agent randomly chooses $k$ of them).

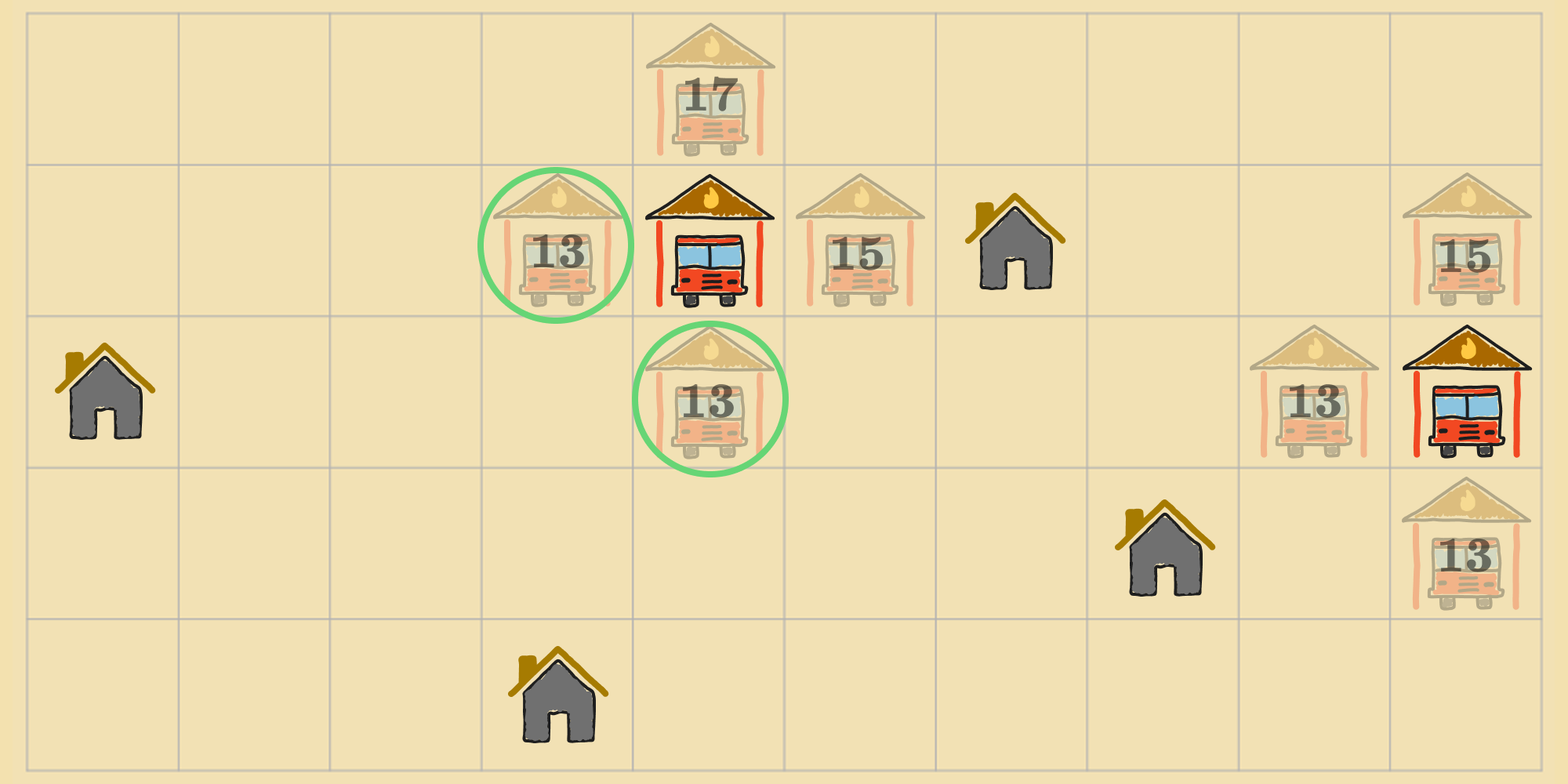
First initial state Possible actions from first initial state

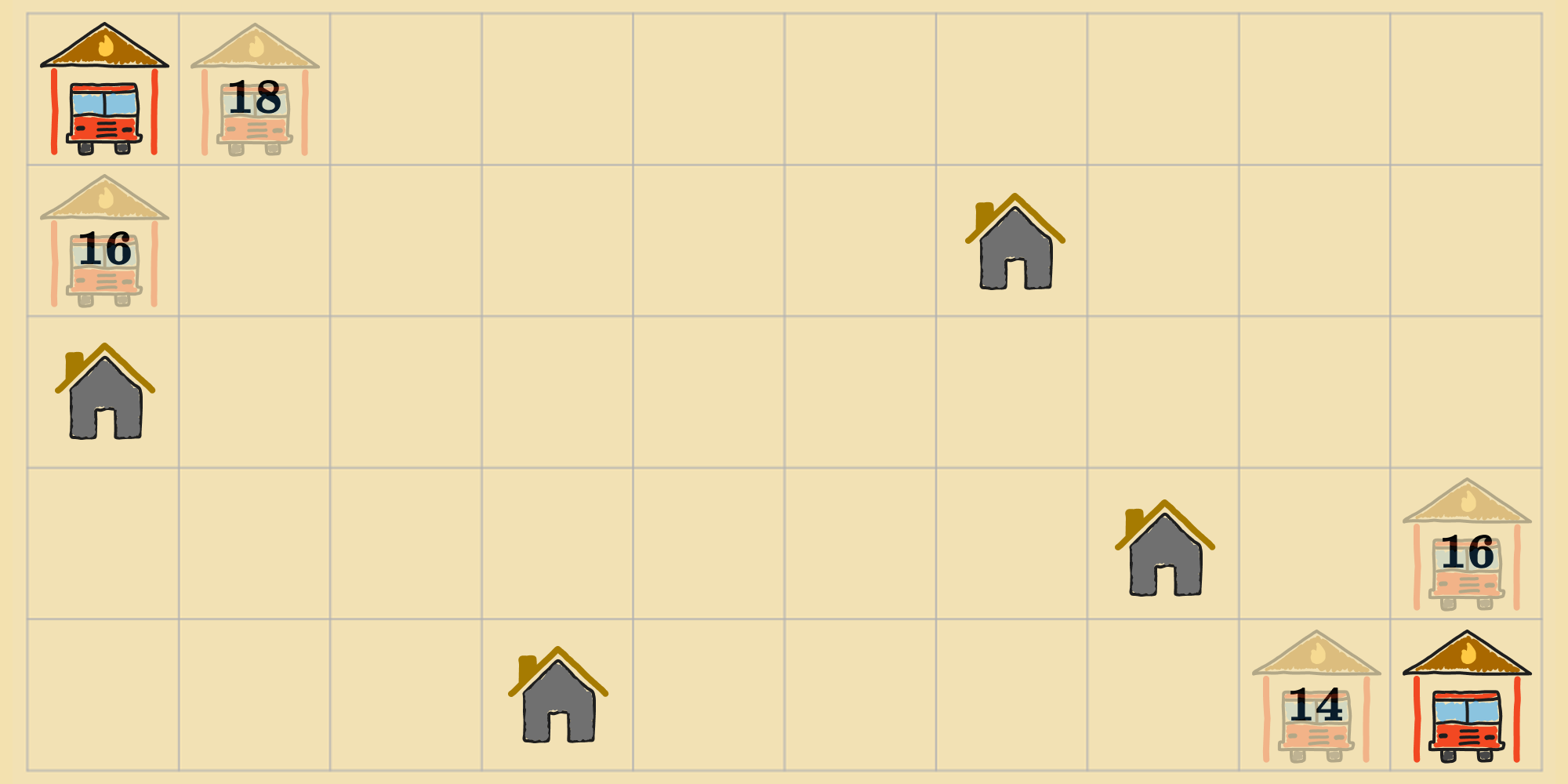
Second initial state Possible actions from second initial state

Then, the agent transitions to the top $k$ neighbors.

First updated state

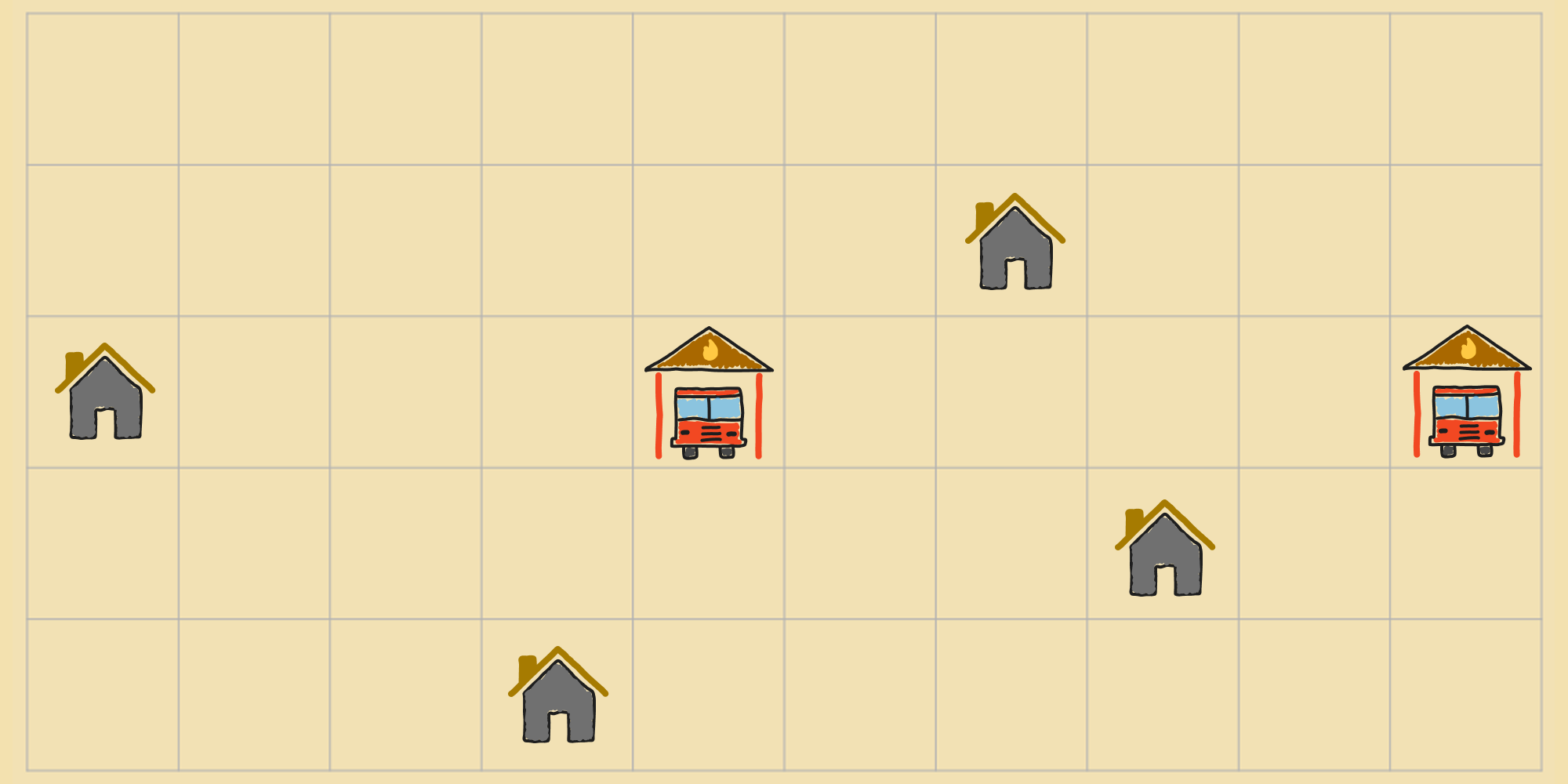
Second updated state

This process repeats until the agent can no longer improve the $k$ states its tracking. Again, this is analogous to how previous algorithms functioned, except that we're applying steps to multiple states simultaneously instead of just one. Here's the version of the local beam search algorithm tailored for objective minimization:

\begin{aligned} &\textbf{function}\ \text{LOCAL-BEAM-SEARCH-MIN}(S_0, f, \text{ACTIONS}, \text{RESULT}, k): \\ &\quad s_1, \ldots, s_k \gets S_0 \\ &\quad \textbf{while}\ \text{true}\ \textbf{do} \\ &\quad\quad N \gets \text{NEIGHBORS}(s_1) \cup \ldots \cup \text{NEIGHBORS}(s_k) \\ &\quad\quad s_1', \ldots, s_k' \gets \arg \min_{s \in N} \text{-k} f(s) \\ &\quad\quad \textbf{if}\ f(s_1') \ge f(s_1) \textbf{ and } \ldots \textbf{ and } f(s_k') \ge f(s_k)\ \textbf{then} \\ &\quad\quad\quad \textbf{return}\ s_1, \ldots, s_k \\ &\quad\quad \textbf{end if} \\ &\quad\quad s_1, \ldots, s_k \gets s_1', \ldots, s_k' \\ &\quad \textbf{end while} \\ \\ &\textbf{function}\ \text{NEIGHBORS}(s, \text{ACTIONS}, \text{RESULT}): \\ &\quad N \gets \emptyset \\ &\quad \textbf{for each}\ a \in \text{ACTIONS}(s)\ \textbf{do} \\ &\quad\quad N \gets N \cup \text{RESULT}(s, a) \\ &\quad \textbf{end for} \\ &\quad \textbf{return}\ N \\ \end{aligned}

The variant for objective maximization is exactly the same, except that we replace the $\arg \min$ with a $\arg \max$ .

Local Beam Search vs Random Restart

At first glance, local beam search seems like its doing nothing more than running $k$ random-restarts in parallel instead of in order. But the two algorithms are quite different if you look closely. In random-restart, each search process runs independently of the others but in local beam search, useful information is passed among the $k$ states, $s_1, \ldots, s_k$ , during each iteration. If $k = 2$ , an agent running random-restart would pluck the best state from $NEIGHBORS(s_1)$ and the best state from $NEIGHBORS(s_2)$ for the next round of search. On the contrary, an agent running local beam search would choose the best $k$ states from $\text{NEIGHBORS}(s_1) \cup \text{NEIGHBORS}(s_2)$ . This gives the agent the ability to abandon some searches in favor of more promising regions where more progress is being made.

Stochastic Beam Search

The greediness of local beam search can lead to a lack of diversity among the $k$ states. If the $k$ states are clustered in a narrow region of the state space, the search reduces to a $k$ -times-slower version of gradient descent or hill climbing. Stochastic beam search, analogous to stochastic gradient descent, helps address this problem. Instead of choosing the top $k$ successors every time, stochastic beam search chooses successors with probability proportional to the successor's value, thus preserving some diversity.