Intro to Search

There are some simple problems where the solution is straightforward. Think about your daily commute to work or school: Starting from your house, you follow the same streets, take the same turns, and—barring any unexpected closures—you arrive without having to reconsider your route each morning. You don't need to figure out the best path each time; you just follow the same procedure—i.e. the same sequence of directions from the starting point to the goal—every day. But there are other problems where the correct move isn't immediately apparent. Consider the invention of the light bulb. Thomas Edison didn't know which filament material would work, so he had to test a lot of different materials until he found one that worked. Search is a family of methods for exploring possible steps or actions in a systematic fashion to discover a path from a starting point to a goal. Let's start by looking at some examples which can be solved using search.

Examples

Maze Navigation

When you're inside of a maze, your objective is to find a path from the entrance to the exit. At each intersection or corridor, you have a set of choices: go north, south, east, or west. You can't see the whole maze at once, so you must explore systematically—backtracking when a path leads to a dead end—to eventually discover a path that leads from the entrance to the exit.

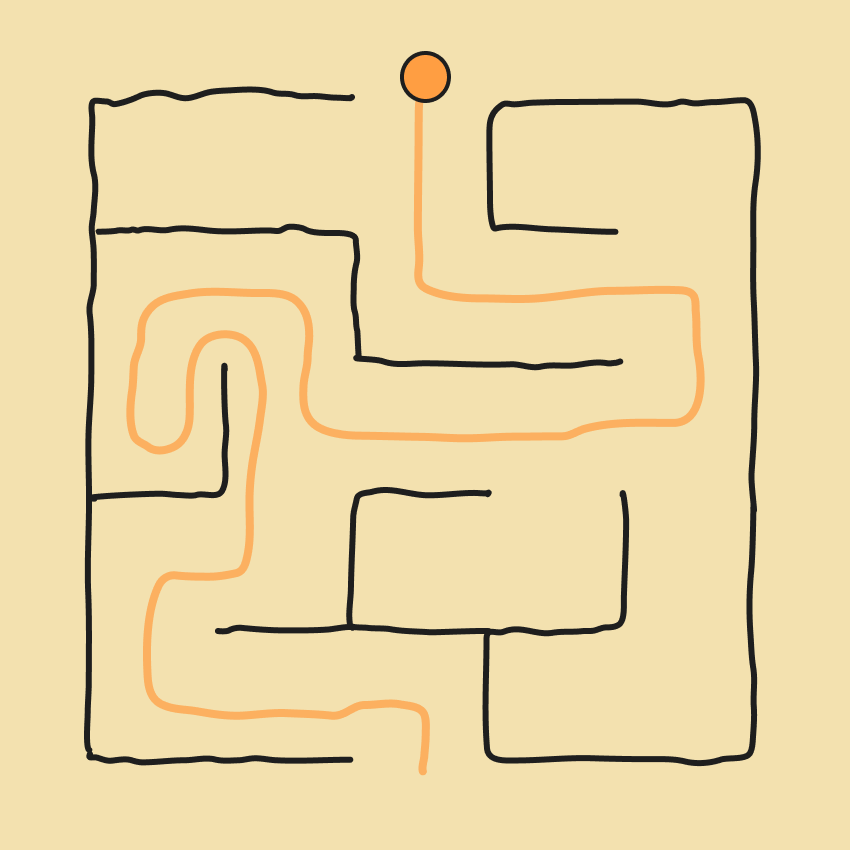
We can formalize this problem as a search problem:

• States: This is any position, $(x, y)$, in the maze you could occupy. Let's denote this set of potential positions, $S$.
• Initial State: The position at the start of the maze. If $s₀$ represents this state, then $s₀ ∈ S$.
• Goal States: The position at the exit of the maze (or positions if there are multiple exits). If $G$ is the set of goal states, then $G ⊆ S$.

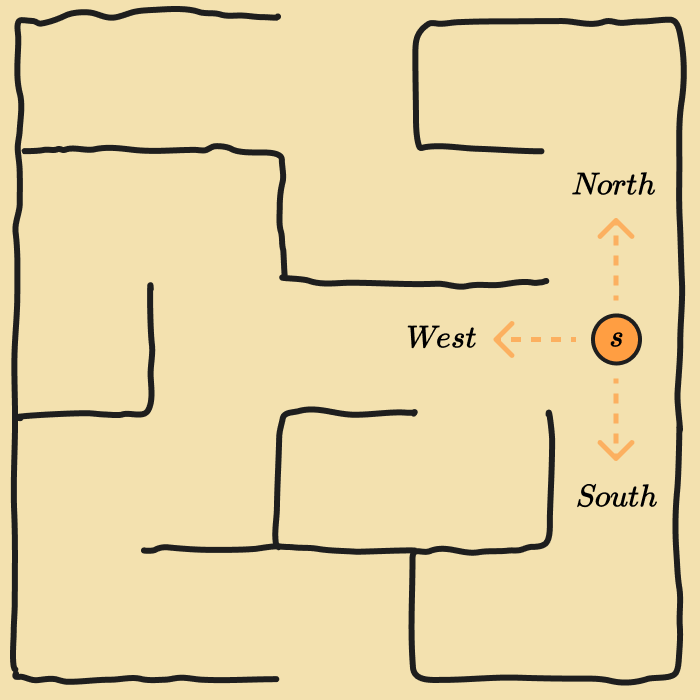
• Actions: Moving north, south, east, or west, depending on your state and which directions are blocked by walls. If $\text{ACTIONS(s)}$ is the set of actions available in state $s$, then $\text{ACTIONS}(s) ⊆ \{North, South, East, West\}$.

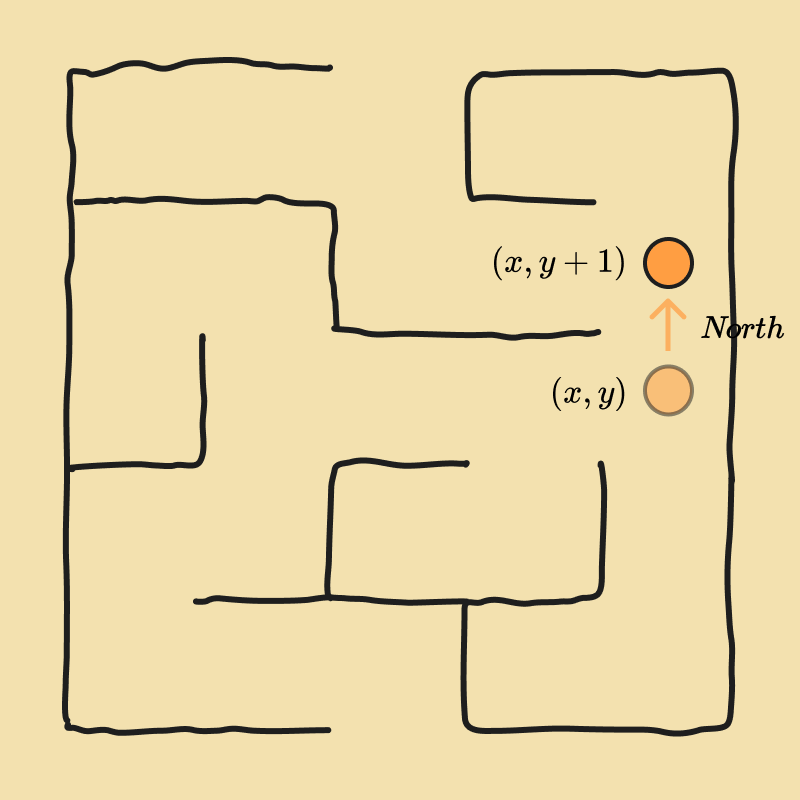
• Transition Model: This describes how the state changes when an action is taken. For example, if you're at position $(x, y)$ and you choose the action $North$, your resulting state would be $(x, y + 1)$. We can write this model as a function, $\text{RESULT}(s, a) → s'$, where $s$ is the initial state, $a$ is the action taken, and $s'$ is the resulting state. So $\text{RESULT}((x, y), North) → (x, y + 1)$.

This simple setting captures the essence of many real-world problems, such as robot navigation and route planning in GPS applications like Google Maps.

Sliding-Tile Puzzle

In a sliding-tile puzzle, a certain number of tiles are arranged in a 2D grid with one empty space. Any tile that's adjacent to the empty space can slide into the empty space, effectively moving the empty space to the tile's previous location. The most popular variant of this puzzle is the 8-puzzle, which consists of a 3 × 3 grid with eight numbered tiles and one blank space. Starting from a scrambled configuration, the goal is to slide the tiles until they're in numerical order.

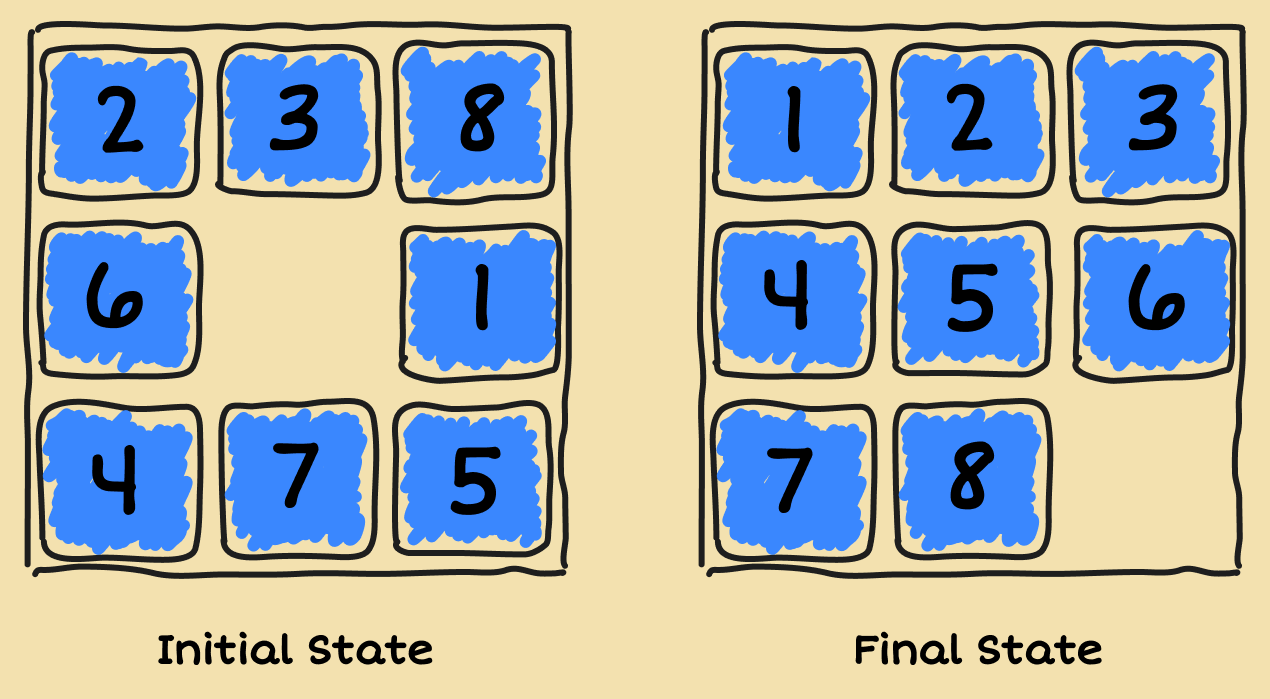
Here's a way to formulate the 8-puzzle as a search problem:

• States: Each state in $S$ corresponds to a specific arrangement of the tiles and the empty space in the grid.
• Initial State: Any state $s ∈ S$ can be designated as the initial state $s₀$. (But it's not possible to reach a goal state from every initial state.)
• Goal States: A set of states $G$ where the tiles are arranged in numerical order.
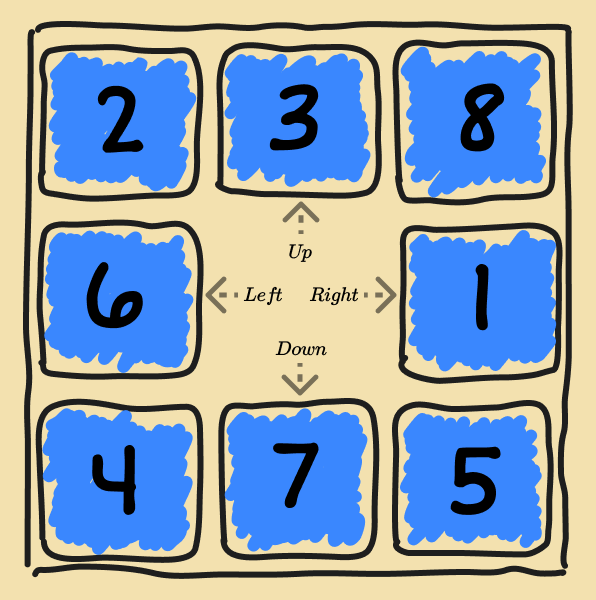
• Actions: When you're physically playing the puzzle, a tile slides into the empty space, but a simple way of describing an action is to think of the empty space moving left, right, up, or down. Of course, if the empty space is next to an edge or corner, then not all actions are valid. $\text{ACTIONS}(s) ⊆ \{Left, Right, Up, Down\}$.

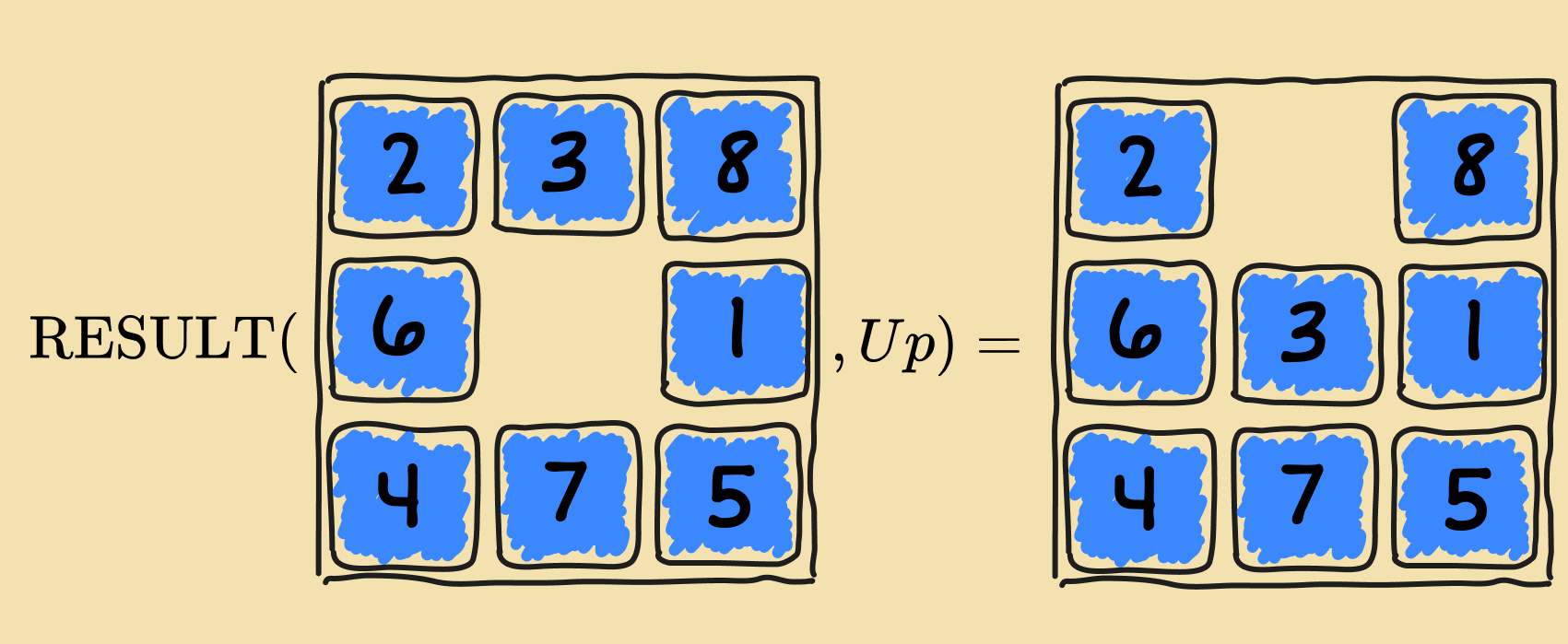
• Transition Model: Maps a state, i.e. a tile configuration, and action, i.e. a move of the empty space, to a resulting state.

What is Search

At its core, search is about finding a sequence of actions that takes an agent from an initial state to a goal state. In any state, rather than guessing randomly, search algorithms explore the space of actions and resulting states methodically, often using strategies that balance completeness (finding any solution) with efficiency (finding the best solution quickly).

Search is not limited to physical movement. It applies to puzzle-solving, scheduling tasks, or even training neural networks (as we'll see later).

Search Problem Formulation

Here's the formal definition of a search problem we've been using:

• States ($S$): The set of all possible states of the environment. Often referred to as the state space.
• Initial State ($s₀$): The starting point of the agent ($s₀ ∈ S$).
• Goal States ($G$): One or more target states in $S$.
• Actions ($\text{ACTIONS}(s)$): For each state $s$, a finite set of actions that can be executed when the agent is in $s$.
• Transition Model ($\text{RESULT}(s, a) → s'$): A function that describes what each action does by mapping a state $s$ and an action $a$, to the resulting state $s'$.

Why do we need a formal definition? By taking problems that we face in the real world and casting them as formal search problems, we can leverage the many existing search algorithms. These algorithms are designed to work off of this formal representation so that we don't have to re-create them for every particular problem we might encounter in the wild.

This formalism is quite handy, allowing us to define almost any problem as a search problem. But that doesn't mean we should always cast problems as search problems. For instance, if you have a well-defined procedure that always works—like your daily commute along the same route—then a procedural script is both simpler and far more efficient. Search becomes valuable when the best path through the state space isn't obvious in advance—when you have many branching choices, uncertain or changing environments, or complex constraints to juggle. In those cases, search can be the optimal approach. Although, as we'll see later, search suffers from various limitations, such as exploding computational costs when the state space is very large and connected.